Probability and Statistics Objectives

1. Probability
   1. Obtain organizational procedures for analyzing data.
      1. Recognize data that can be classified as empirical.
      2. Conduct a random sample experiment by describing and selecting a sample from a population.
      3. State the definition for simple and compound events; list examples of each kind of event.
   2. Make reasonable conjectures from purely chance phenomena.
      1. Express the probability of an event as a fraction.
      2. State the definition for the probability of an event.
      3. Compute the probability of an event, P(E), in a finite sample by summing the probabilities of the sample points in the event.
   3. Acquire an efficient method for counting arrangements of objects.
      1. Identify permutations and combinations as counting events in a sample.
      2. Use the permutation and combination theorems in problem solving.
   4. Describe relationships between two or more events.
      1. Classify two or more events as one or more of the following:
         1. complementary
         2. conditional
         3. dependent
         4. independent
         5. mutually exclusive
      2. State the definition for the conditional probability of two events A and B as: P(B/A) = P(AB)/P(A) or P(A/B) = P(AB)/P(B).
      3. Prove that two events are independent if either P(A/B) = P(A) or P(B/A) = P(B).
   5. Predict the outcome of a combination of events given the results of at least one of those events.
      1. Compute the conditional probability of two events that are either dependent or independent.
      2. Use the following laws of probability in calculating the probability of a compound event:
         1. additive: P(A + B) = P(A) + P(B) - P(AB)
         2. multiplicative: P(AB) = P(A)P(B/A) or P(B)P(A/B)
2. Mathematics of Apportionment
   1. Express sums in a concise form.
      1. Use correctly the symbol Σ
      2. Use the following theorems as they apply to a given sum:

         1. n
            Σ	c = nc
            i=1

         2. td align=center>n

            n
            Σ	cxi = n	Σ	xi
            i=1		i=1

         3. n		n		n		n
            Σ	xi + yi - zi =	Σ	xi +	Σ	yi -	Σ	zi
            i=1		i=1		i=1		i=1

   2. Report the information contained in data.
      1. Prepare and use histograms.
      2. Use the terms “population” and “sample” correctly.
      3. Find for a given experiment the following measures of central tendency:
         1. mean [ 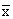(sample), μ (population)]
         2. median
         3. mode
      4. Find for a given experiment the following measures of variability:
         1. range
         2. variance [ s² (sample variance with (n-1) degrees of freedom), σ² (population)]
         3. standard deviation [ σ (population), s (sample)]
      5. Compute the mean and the sample variance, when given a population sample.
      6. Use the sample mean and the sample variance to estimate the population mean and population variance.
      7. State and apply the empirical rule as the rule relates to Chebyshev's theorem.
3. Probability Distribution
   1. Apply the past success of an event to future trials.
      1. State the four requirements for a binomial experiment.
      2. Derive the binomial probability distribution
      3. Compute the binomial probability distribution for a given experiment.
      4. Compute the mean and standard deviation for the binomial variable in a given binomial experiment.
   2. Minimize the chance of error in accepting or rejecting a given hypothesis.
      1. Construct graphically the operating characteristic curve for a given sampling plan.
      2. Define for a given experiment the following:
         1. null hypothesis (H₀)
         2. acceptance region
         3. rejection region
         4. Type I errors (α) and Type II errors (β)
4. Statistical Inference
   1. Draw useful inferences from samples applied to the normal distribution.
      1. State the central limit theorem and apply the theorem to a given experiment.
      2. Construct the normal probability distribution curve and interpret its tabulated values as areas lying within a specified number of standard deviations of the mean.
      3. Approximate the binomial distribution by use of the normal distribution and compute the following for a given experiment:
         1. values of z (the standardized normal variable)
         2. probabilities for x (the random variable)
         3. probability of a Type I error and location of the rejection region
         4. probability of a Type II error and location of the acceptance region
      4. Distinguish between a confidence interval and a confidence coefficient.
   2. Demonstrate successful sampling procedures to evaluate a hypothesis.
      1. State the hypothesis to be tested.
      2. Select the sample.
      3. State the alternative hypothesis.
      4. Evaluate Type I or Type II errors.
5. Enrichment Objectives
   1. Demonstrate successful sampling procedures to evaluate a hypothesis involving two populations by completing each of the following:
      1. Test a hypothesis concerning µ (the mean) of two populations by use of the student’s distribution.
      2. Compute and make inferences from small samples concerning the difference between two means.
      3. Identify the Chi-square probability distribution and the F-distribution and interpret tabulated values for each kind of distribution.
      4. Draw inferences from the variance of two given populations by using the Chi-square test and the F-test.
   2. Linear Regression and Correlation
      1. Use a straight line as a predictor for the outcome of an experiment.
      2. Construct a scatter plot for a given experiment.
      3. Obtain a prediction equation for a given experiment by use of the scatter plot and a line of “best fit.”
      4. Use the least squares method to find the “best” fitting line for a given set of points.
      5. Compute and analyze the variance of the random error of the deviation from the regression line by using the data from a given experiment.
      6. Use the regression equation y = β₀ + β₁x to:
         1. Test H₀: β1 = 0 against H : β₁ ≠ 0.
         2. Estimate the slope β₁.
         3. Compute the expected value of y, given x[E(y/x)].
      7. Compute the coefficient of correlation between y and x for a given line.
      8. Define and use a prediction equation for a given experiment.